The Online RREF Calculator and Echelon Form of Matrices
Table of Contents
The Row Leading Number:
The learning number in the row is the number coming before or after the “0”. It may possible that the leading number is appearing at the third or the fourth place of a matrix.
You can understand the landing number by the given example:
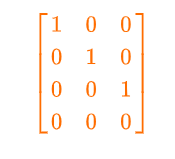
In the first row, the learning number is “1” which is appearing in the first row of the matrix. The leading number in the second row is coming at second place and in the third row, it is coming at third place.
The Pivot Element?
The first non-zero element in the first row of the matrix is known to be the pivot element of the echelon form matrix. The non-zero element should come after the pivot element of the echelon form matrix
The Zero Row:
The Zero Row of the matrix should be the bottom of the matrix to fulfill the other condition of the echelon form matrix. If the zeroth row is placed in the middle of the matrix, then we would not consider the matrix as an echelon form matrix. When you are using the RREF calculator, it would automatically fulfill all the conditions of the echelon form matrices.
How to Find the Echelon Form Matrix?
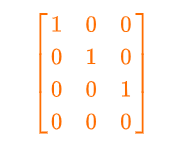
The Echelon Form Matrix form of the given matrix can be determined by the following procedure. You need to enter the elements in the RREF calculator and find the echelon form of the matrix.
- Divide the first row by the “3”, then make the leading element in the first row equal to “1”.
- Then abstracted the second row by the 7R1 to make the leading element in the second row equal to the 1.
- Now subtract both rows from each other to convert the matrix to the echelon form a matrix.
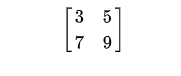
Every solution of the linear equations can be transformed into another form or method that has an identical set of solutions. There is a possibility a set of linear equations can be solved easily by the echelon form methodology. We usually adopt much more straightforward methods to solve a set of linear equations. You can find the solution by making the rows of the matrix with the assistance of the reduced row echelon form calculator.
Conditions of the Echelon Form Matrix:
If you have a matrix and want to convert it into the RREF form, then follow the conditions to make it into the echelon form:
- Make the first number in each row equal to “1”
- The next lending number should be one step towards the right to the upper row.
- All the rows containing the non-zero entities should be placed on the above side of the zero rows.
Zero Matrix and Echelon matrix:
The bottom lines can have zero rows but the whole matrix in the echelon form can’t be the zero matrices. The leading element should be equal to “1” as if all the elements in the matrix are equal to zero, then it would be a null matrix not. The other thing is the “1” appearing in the second row should appear at the right bottom of the first learning number.
The Reduced Echelon Form of Matrix:
The Echelon form of a Matrix can be easily converted to the reduced echelon form of a matrix by applying the row operation technique. You can also apply the row operation by the RREF calculator to find the reduced echelon form of a matrix. There can be different forms of echelon and reduced echelon forms of the matrix as the symmetry would be different
Conclusion:
In linear algebra, you may need to convert the linear algebraic equation into the echelon or the reduced echelon form. You can find the echelon form matrix of the linear equation by the RREF calculator. You just need to enter the coefficient of the linear equation in the online tool.
